Triple Phytagoras

Kita semua pasti sudah mengenal rumus phytagoras yaitu $a^2 + b^2 = c^2$ dengan $c$ adalah sisi terpanjang. Tapi akankah terpikirkan kalau kita menemukan angka - angka pasangan yang memenuhi rumus phytagoras tersebut tanpa ada panjang sisi yang berbentuk bilangan desimal (berkoma)sebagai contoh 3, 4, 5. Tentu ini merupakan hal yang lumayan tidak mudah.

Tidak tahu apa yang ada dalam pikiran saya sehingga saya mencoba mencari cari beberapa pasangan bilangan triple phytagoras, untuk sebagian orang hal ini mungkin adalah hal yang kurang kerjaan hehehe. Setelah beberapa menit saya telah mendapatkan beberapa pasangan triple phytagoras seperti gambar di bawah ini. mungkin bagi anda semua yang mungkin tidak percaya silahkan cek saja dengan menggunakan rumus phytagoras (kalau mau).

x= sisi pertama segitiga
y= sisi kedua segitiga
z= sisi terpanjang segitiga (hipotenusa)

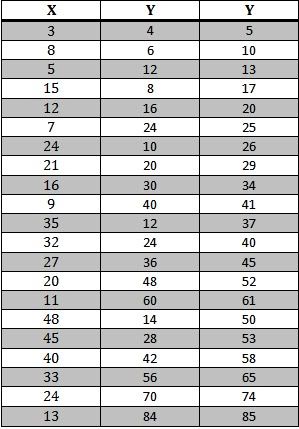bagaimana dengan anda???!!! apakah anda bisa mendapatkan pasangan triple phytagoras yang lainnya??? jangan takut dan jangan ragu saya pastikan anda pasti bisa!! mau tau caranya??!!

Gunakan Rumus ini:

\[x = m^2 - n^2\]
\[y = 2mn\]
\[z = m^2 + n^2\]

Tugas anda hanya mengganti m dan n dengan bilangan yang anda pilih. Misal $m=2$ dan $n=1$ maka akan menghasil kan 3, 4, 5. Selamat Mencoba