Sedikit Coretan

Banyak kejadian-kejadian atau momen-momen yang sebenarnya bisa diceritakan disini tapi sayang hanya beberapa momen yang bisa dijadikan artikel, salah satunya adalah artikel yang sedang anda baca ini akan menceritakan sedikit tentang Aksioma Bilangan Asli.

kita ketahui bahwa Aksioma adalah suatu kesepakatan yang sudah tidak lagi di ragukan kebenarannya dan bilangan asli (bulat positif) adalah bilangan yang dimulai dari 1,2,3,4... sampai tak hingga. Kalau kita cari tahu tentang hal ini (sebelum menjadi aksioma bilangan asli) sebenarnya bilangan asli ini sendiri tidak ada yang dapat membuktikannya dan juga tidak ada yang dapat membantah.

Hal inilah yang membuat bilangan asli hanya di sepakati saja (akskioma) tapi ada embel - embel di belakangnya yaitu "yang tidak di ragukan lagi kebenarannya" hehe.

Hal yang menarik disini adalah jikalau ada orang yang dapat membantah bilangan asli itu berarti semua rumus, teorema dsb yang ada dalam matematika akan berguguran. Hal ini dikarenakan semua rumus, teorema matematika didasarkan pada bilangan asli. Apakah anda salah satu orang yang berminat untuk membantah konsep bilangan asli??? jika terbukti anda dapat membantahnya nama anda pasti akan di abadikan dalam sejarah matematika.

MAU???

Pembuktian Bilangan Irrasional

Tidak terasa minggu kedua bulan ini pun sudah lewat dan kali ini baru bisa posting lagi, maaf buat para pembaca setia yang mungkin menunggu terlalu lama blog ini update hehe (harap maklum).Untuk kelanjutan blog ini mungkin akan terus membahas pembuktian dan pembuktian matematika. Karena itulah pekerjaan orang yang bergelut di bidang matematika.

Sebelum masuk ke pembuktian ada baiknya cerita - cerita sedikit tentang bilangan karena berguna pada saat kita membuktikan bilangan irrasional. Dalam sistem bilangan, bilangan real di bagi menjadi dua yaitu bilangan rasional dan irrasional. Oke langsung saja bilangan-bilangan rasional adalah bilangan yang dapat di tuliskan dalam bentuk $\frac{m}{n}$, dengan $m$ dan $n$ adalah bilangan-bilangan bulat dengan $n\not=0$.Sebaliknya Untuk Bilangan irrasional tidak dapat di tuliskan sebagai suatu hasil bagi dari dua bilangan bulat.

Rataan Aritmetik VS Rataan Geometris

Waaah akhirnya bisa posting lagi nih, setelah kurang lebih setengah bulan tidak aktif di blogger hehe. Ini semua di karenakan tidak adanya koneksi internet di kost-an dan kendala laptop yang lagi cerewet!! kok jadi curhat ya.

Oke kembali ke pokok judul artikel ini. Sebelumnya saya pernah membahas tentang rataan aritmetik dan rataan geometris yang belum baca silahkan di baca dulu, kalau sudah dibaca sekarang saatnya kita adu mereka berdua hehe. Diadu disini maksudnya adalah siapa yang lebih besar dan siapa yang lebih kecil??!!

Apakah Benar Semua Bilangan Pangkat Nol Sama Dengan Satu??

Dilihat dari judulnya kok panjang banget ya hehe, ya memang begitu adanya. Banyak kita dengar khususnya dari murid SMA mengatakan bahwa semua bilangan bila di pangkat nol sama dengan satu. Hmmm apa betul yaa??!! Apa sudah di periksa benar – benar pernyataanya itu??. Dan bagaimana dengan membuktikan kalau bilangan di pangkatkan nol samadengan satu??!!. Duh duh duh semakin banyak pertanyaan yang timbul dan wajib dibuktikan jadinya!!.

Sebelum saya menjawab pertanyaan dari judul diatas ada baiknya kita buktikan terlebih dahulu beberapa bilangan di pangkatkan nol sama dengan satu. Disini Math Jitu akan membuktikan dengan menggunakan salah satu sifat eksponen yaitu.

Triple Phytagoras

Kita semua pasti sudah mengenal rumus phytagoras yaitu $a^2 + b^2 = c^2$ dengan $c$ adalah sisi terpanjang. Tapi akankah terpikirkan kalau kita menemukan angka - angka pasangan yang memenuhi rumus phytagoras tersebut tanpa ada panjang sisi yang berbentuk bilangan desimal (berkoma)sebagai contoh 3, 4, 5. Tentu ini merupakan hal yang lumayan tidak mudah.

Tidak tahu apa yang ada dalam pikiran saya sehingga saya mencoba mencari cari beberapa pasangan bilangan triple phytagoras, untuk sebagian orang hal ini mungkin adalah hal yang kurang kerjaan hehehe. Setelah beberapa menit saya telah mendapatkan beberapa pasangan triple phytagoras seperti gambar di bawah ini. mungkin bagi anda semua yang mungkin tidak percaya silahkan cek saja dengan menggunakan rumus phytagoras (kalau mau).

Pembuktian Rataan Geometris

Menyusul pembuktian aritmetik sekarang akan di bahas pembuktian geometris!!!. Bilangan $\sqrt{ab}$ dinamakan rataan geometris dari dua bilangan positif $a$ dan $b$, tidak henti - hentinya kami sarankan kepada pembaca semua alangkah baiknya di coba terlebih dahulu bagaimana cara membuktikannya ok!!.

Pembuktian Rataan Aritmetik

Bilangan $\frac{1}{2} (a + b)$ dinamakan rataan aritmetik dari $a$ dan $b$ dengan $a < b$. Berikut ini akan kita bahas pembuktian apakah benar $\frac{1}{2} (a + b)$ adalah rataan aritmetik dari $a$ dan $b$. Kalau anda lihat pembahasan ini secara langsung mungkin anda beranggapan bahwa ini adalah hal yang mudah!! tapi saya sarankan anda untuk mencoba dulu sendiri, ambil pensil dan corat coret dulu hehe.

Jangan Anggap "Enteng" Angka NOL

Ada apa dengan angka Nol?? apa jadinya kalau angka 10 tanpa angka 0, itu berarti hanya 1. Sekiranya sangat jauh perbedaannya, apalagi kita coba dengan angka yang lebih besar tentu perbedaannya juga lebih besar. Angka nol ini sendiri memiliki perjalanan yang sangat panjang hingga akhirnya resmi untuk menggunakannya.

angka nol "ada" berkat karya al-khwarizmi (780 - 850) seorang matematikawan asal Irak yang terkenal dengan karyanya Al-jabr wa’l muqabala (yang kemudian menjadi ilmu legendaris yaitu Aljabar). Karena sang penggagas angka nol berasal dari Irak (Negara Arab) tentulah angka nol lebih di kenal di negara-negara arab, akhirnya angka nol di bawa ke Eropa oleh Fibonnaci. Karena alasan Agama (menyinggung) membuat angka nol kembali tenggelam, dan muncul kembali setelah Rene Descartes dengan Kartesian nya yang menggunakan angka nol pada titik pangkal/asal/origin.

Si "ABC" yang Familiar

Pasti kita sudah tahu dengan rumus matematika yang satu ini, yaitu rumus yang sering kita sebut rumus ABC. Rumus ini digunakan untuk mencari bilangan x dari suatu persamaan kuadrat:

$ax^2 + bx + c = 0$ dengan $a \not=0$ nilai $x_1$ dan $x_2$ sebagai berikut:
\[x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

Dikarenakan persamaan kuadrat maka hasil dari persamaan itu adalah dua buah yaitu $x_1$ dan $x_2$. Rumus ini mungkin kita sudah ketahui sejak duduk di bangku SMP tapi tahukah anda bagaimana rumus ini didapat?jangan takut di sini akan di jelaskan bagaimana rumus ini diapat. Mari kita kupas satu persatu.

Gradien Suatu Garis Lurus

Gradien disebut juga “koefisien arah” dengan notasi $m = \tan \alpha$ ($\alpha$ adalah sudut antara garis dan sumbu x positif) .

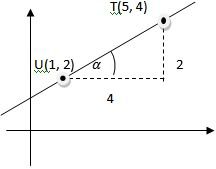Perhatikan gambar di samping, misalkan titik T(5, 4) dan U(1, 2) berada pada suatu garis lurus maka gradiennya adalah:
\[m = \tan \alpha = \frac{2}{4} \]

Teorema Phitagoras

Pastinya kita sudah mengetahui rumus phitagoras yang paling terkenal yaitu $a^2 + b^2 = c^2$ tapi akankah kita memikirkan bagaimana membuat pemodelan untuk membuktikan rumus tersebut. Nah disini akan kita ulas tentang pemodelan tersebut !!. Bagaimana sudah siap untuk berlayar??!! Hehe memangnya mau kemana ya pake’ berlayar segala!!.